住宅ローンなどにおいて一定期間経過したときに元金がいくらに減っているのかを計算します。繰上げ返済などを行うときの参考にもなります。
計算式
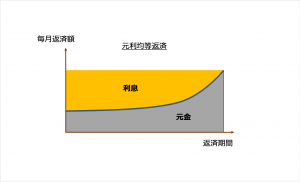
ローンの返済方式は一般的な元利均等で返済することが前提
- r ：月々の金利（年利を12で割ったもの）
- n ：ローンの総返済回数（年数を12で掛けたもの）
- k ：これまでに返済した回数
毎月の返済額を次の計算式から求めます。
毎月の返済額から利息部分と元金部分の支払額を計算して残りの元金を計算します。支払った分だけ繰り返します。
月の利息 = 返済額 x 月の金利
月の元金部分 = 毎月の支払額 – 月の利息
残りの元金 = 返済額 – 月の元金部分
計算例
例）次のような条件の時の元金の残高はいくらになるか
- r ：0.3% / 12 = 0.00025
- n ：35年 x 12 = 420
- k ：6年 x 12 = 72
月の返済額 = 75,253円
月の利息 = 30,000,000 x 0.00025 = 7,500円
月の元金部分 = 75,253 – 7,500 = 67,753
残りの元金 = 30,000,000 -67,753 = 29,932,247円
これを６年間として72回繰り返します。手計算ではとても面倒なのでエクセルやプログラミングで計算が必要です。
6年後の元金 = 25,078,229円
コメント